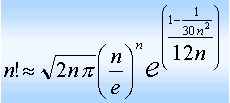这是我的第一篇正式论文,是看过一本数学科普书中的公式之后搜索资料写成的,但自己进行了很大的探索,是前人所没有涉及的内容。这篇论文不是单纯的介绍一种公式,而是对公式进行探索,通过试验寻找适合的更精确的处理方式,并运用于计算机算法。这种思想叫做“数学实验”,是在计算机帮助下进行的实用数学研究。
另外,从本文的内容来看,开创了一种精确度很高的阶乘运算方式,也是一大突破。精确度在14位以上,而运行时间消耗几乎没有。
这里提供了一个下载包,压缩后101kb,其中包括论文(370k),pascal源程序,exe计算程序。
html版:http://heymu.com/t/use-stirling-do-factorial-by-myheimu.htm
word版:http://heymu.com/t/Using-Stirling-do-factorial-by-Myheimu.doc
计算程序:http://heymu.com/t/factorial.exe
计算源代码(pascal):http://heymu.com/t/factorial.pas
所有内容打包文件(不包括Pascal源代码):http://heymu.com/t/Using-Stirling-do-factorial-by-Myheimu.rar
希望大家批评指教!
用Stirling逼近近似计算阶乘的探讨与应用
江苏省连云港市赣榆高级中学 仲晨
【关键词】: Stirling逼近,阶乘,极限论,微积分,数学实验,计算机算法